Szilvi néni matek lapja
Hasonlóság
1.) Készítsd el négyzetrácson a rajzok megfelelő arányú hasonló képét!
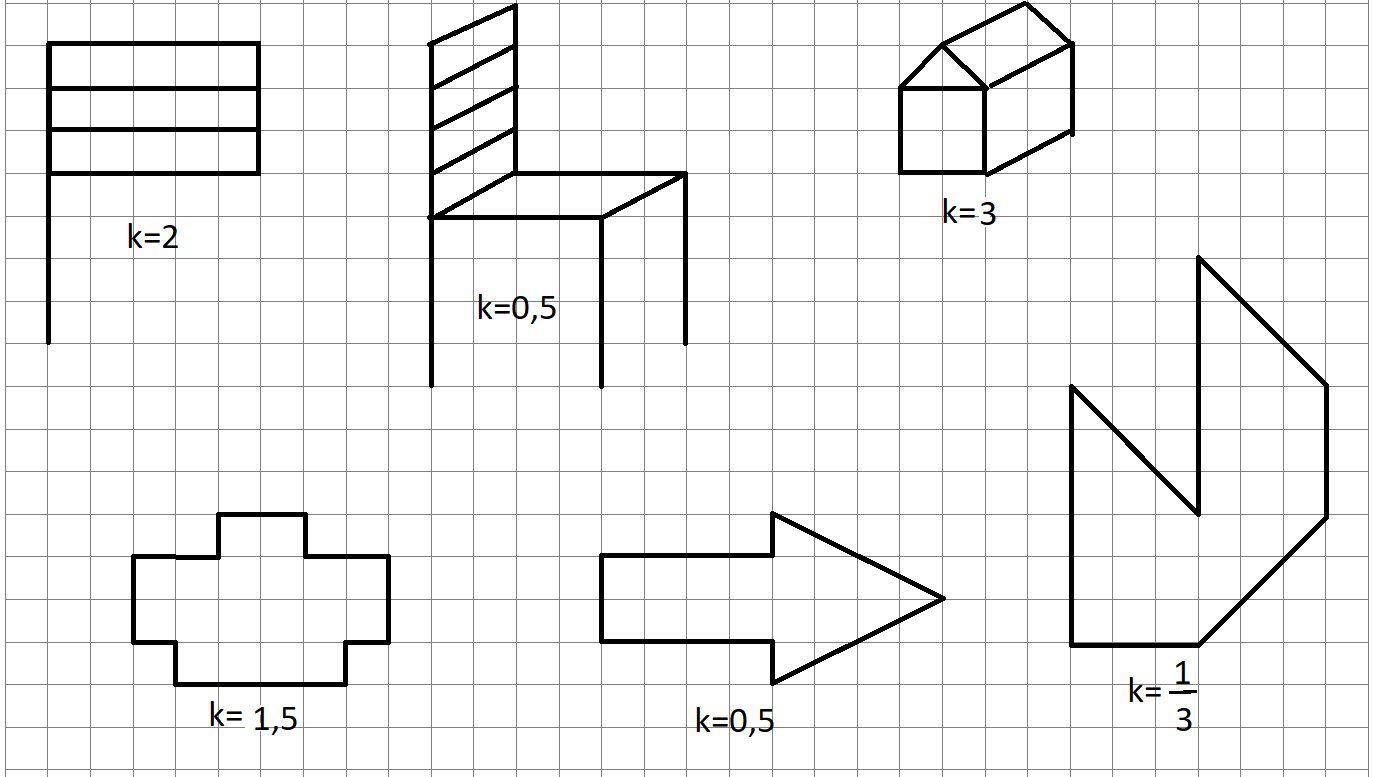
2.) Méretarányos feladatok
- Egy térkép méretaránya 1:500. Milyen hosszú a valóságban a híd, ha a térképen 3,6 cm-nek mértem? Milyen széles a térképen a folyó, ha a valóságban 8 m?
- Az 1:500 000 méretarányú térképen Kecskemét és Szeged távolsága 15 cm hosszú szakasz. Hány kilométerre van a két város egymástól légvonalban? Ugyanezen a térképen hány cm-nek mérhető a Győr-Budapest közötti 105 km-es távolság?
- Egy rovar nagyított képének méretaránya 20:1. Mekkora a rovar csápjának a hossza a képen, ha a valóságban 3 mm? Milyen hosszú a valóságban az a rovar, amelyik a képen 15 cm hosszú?
- A H0-s modellvasút 1:87 arányú szerelvényeket tartalmaz. Egy M62-es dízelmozdony makettje 200 mm. Hány méter hosszú a valóságban a mozdony?
- Egy térkép méretaránya 1:700 000. Mekkora a valóságban az a távolság, ami a térképen 3,2 cm? Mekkora a térképen az a távolság, amelyik a valóságban 37,1 km?
- Egy térképen két település távolsága 5,2 cm. Mekkora a valóságban ez a távolság, ha a térkép méteraránya 1:25.000? Mekkora a térképen annak a két településnek a távolsága, amely a valóságban 7,8 km-re van egymástól?
3.) Hasonló-e? Miért?
- Egy 3 cm és egy 8 cm sugarú kör?
- Egy háromszögről azt tudjuk, hogy két szöge 45 és 56 fokos. Egy másik háromszögnek van egy 79 és egy 56 fokos szöge. Hasonló-e a két háromszög?
- Két háromszög közül az egyiknek az oldalai: AB = 3,2 cm, BC = 6,4 cm és AC = 4,8 cm, a másiké EF = 4,8 cm, FG = 2,4 cm, és EG = 3,6 cm. Igaz-e, hogy a két háromszög hasonló? Ha igen, akkor mely oldalak és csúcsok felelnek meg egymásnak?
- Két négyszög, ha az egyik oldalai sorrendben 3 cm, 4,5 cm, 3,2 cm és 5,5 cm, valamint a másik oldalai ugyanabban a sorrendben 6 cm, 9 cm, 6,4 cm és 11 cm?
- Egy olyan deltoid, amelynek oldalai 8 cm és 3 cm-esek illetve egy olyan deltoid, amelynek oldalai 4 cm-esek és 1,5 cm-esek?
- Két rombusz, ha az egyik oldalai 6 cm-esek, a másik oldalai 3,6 cm-esek?
4.) Hiányzó oldal kiszámítása I. A műveletet is írd fel, ne csak a végeredményt!
- Egy háromszög oldalai: a= 3 cm, b=6 cm, c= 7 cm. Mekkorák a hozzá hasonló háromszög oldalai, ha k=2,2?
- Egy négyzet oldalai 6 cm-esek. Mekkorák a hozzá hasonló négyzet oldalai, ha k=0,7? Hasonlítsd össze a két négyzet kerületét, területét!
- Egy téglalap oldalai: a=3,6 cm, b=8 cm. Mekkorák a hozzá hasonló téglalap oldalai, ha k=4. Hasonlítsd össze a két téglalap kerületét, területét!
- Egy kocka élei a=5 cm-esek. Egy másik kocka élei ennek 2-szeresei. Hasonlítsd össze a kockák felszínét, térfogatát!
- Egy téglalap oldalai a=3 cm, b=9 cm. Mekkora a hozzá hasonló téglalap hosszabb oldala, ha a rövidebb oldala 7 cm?
- Egy deltoid oldalai a=2,6 cm, b=5,2 cm. Mekkora a hozzá hasonló deltoid rövidebb oldala, ha a hosszabb oldala 18,4 cm?
5.) Hiányzó oldal kiszámítása II.
- Egy háromszög oldalai a= 4 cm, b=6 cm, c=7 cm. A hozzá hasonló háromszög a’ oldala 16 cm. Mekkora a hasonlóság aránya? Mekkora a hasonló háromszög másik két oldala?
- Egy húrtrapéz oldalai: a=10 cm, b=d=6 cm, c=4 cm. A hozzá hasonló trapéz szárai 13,2 cm-esek. Mekkora a hasonlóság aránya? Mekkorák a hasonló trapéz alapjai?
- Egy téglalap alakú fénykép mérete 9x13 cm. Ezt szeretném felnagyítani úgy, hogy a rövidebb oldala 15 cm legyen. Mekkora a hasonlóság aránya? Mekkora lesz a hosszabb oldala?
- Egy háromszög oldalai: 3 cm, 3,5 cm és 4,5 cm. Egy hozzá hasonló háromszög kerülete 33 cm. Mekkorák az oldalai?
- Egy egyenlő szárú háromszög alapja 15 cm, egy hozzá hasonló háromszög alapja 25 cm. Határozd meg a két háromszög oldalait, ha a kisebb háromszög kerülete 33 cm.
- Egy téglalap oldalai a=3 cm és b=4 cm. A hozzá hasonló téglalap átlója 7,5 cm. Mekkorák a hasonló téglalap oldalai?
6.) Szöveges feladatok
- A történetírók szerint Thalész árnyékuk segítségével mérte meg a piramisokat úgy, hogy leszúrt egy botot a földbe, és kifigyelte azt a pillanatot, amikor azonos hosszúságú a bot és az árnyéka. Ekkor a piramis árnyéka is egyenlő a magasságával. Peti a testmagasságát akarja hasonló módszerrel megmérni. Leszúr egy botot a földbe, aminek 51 cm-es darabja áll ki. Az árnyék hossza 34 cm. A saját árnyéka 119 cm hosszú. Milyen magas Peti?
- A festők kinyújtott karjukkal méregetik az arányokat a ceruzájukon. Mekkorának méri az 196 centiméteres modellt a festő, ha az tőle 4,8 méterre van, és a ceruzával a szemétől 60 cm-re mér?
- Egy fényképész a múzeumban egy 150 cm magas képről szeretne fotót készíteni úgy, hogy az egész kép magassága látható legyen a fotón.
 A fényképezőgépében 35 mm magas a film, amin a kép keletkezik, és a film az objektívtől 100 mm-re található. Milyen messze tegye a fényképezőgép állványát a képtől?
A fényképezőgépében 35 mm magas a film, amin a kép keletkezik, és a film az objektívtől 100 mm-re található. Milyen messze tegye a fényképezőgép állványát a képtől? - – e. Mekkora az ábrán látható fa magassága, ha a következő adatokat ismerjük:

Hasonlóság
Az órák tartalma
- (H) Hasonlóság fogalma, aránya, háromszögek, sokszögek hasonlósága
- (K) Hasonló síkidomok hiányzó adatának meghatározása (Hasonló síkidomok területének, térfogatának aránya)
- (SZ) Középpontos hasonlóság (fogalma, tulajdonságai)
- (CS) Középpontos hasonlóság szerkesztése k<0
- (H) Középpontos hasonlóság szerkesztése k>0 (nyújtás szerkesztése)
- (K) Középpontos hasonlóság felhasználása (számítások, szakasz részekre osztása)
- (SZ) Gyakorlás/Beadandók órai bemutatása
- (CS) Összefoglalás
- (H) Témazáró dolgozat
Pontszerzési lehetőségek
- Bemutató készítése Max 2 db Csak leadva 1 pont, felolvasva 2 pont, fejből mondva 3 pont, visszakérdezve 4-5 pont
Témakörök:- hasonlóság fogalma
- háromszögek hasonlósága
- hasonló síkidomok területének, térfogatának aránya
- hasonlóság a való életben
- középpontos hasonlóság és tulajdonságai
- középpontos hasonlóság megjelenése a való életben
- Hasonlóság témakörben:
- felelés --- 2 pont
- hasonló alakzatok rajzolása négyzetrácson --- 2 jó feladat = 1 pont Max 3 pont
- hiányzó oldal - k adott --- 2 jó feladat = 1 pont Max 3 pont
- hiányzó oldal - a' adott --- 2 jó feladat = 1 pont Max 3 pont
- méretarány --- 2 jó feladat = 1 pont Max 3 pont
- hasonló-e? --- 2 feladat = 1 pont Max 3 pont
- szöveges feladatok --- 1 feladat = 1 pont Max 5 pont
- Középpontos hasonlóság témakörben:
- felelés --- 2 pont
- szerkesztés – 1 szerkesztés = 1 pont (1 típus – 1 pont!) Pontok jóváhagyásának feltétele: Órán egy általam választott feladat megoldása
- Tetszőleges négyszög 3 középponttal (kívül, csúcsban, belül)
- k=+2
- k=+0,5
- k=+1,5
- k=-2
- k=-0,5
- k=-1,5
- más tetszőleges k-val és tetszőleges kp-tal max 3 pont
- szakasz 3; 5; 6; 7 egyenlő részre osztása bármelyik – max 3 pont
- Tetszőleges négyszög 3 középponttal (kívül, csúcsban, belül)
- Órai munka 1-1 pont összesen 8 pont
- Dolgozat 50 pont (% felezve)
- Egyéb: aktuálisan meghatározva
Összesen eddig elérhető 113 pont.
Ponthatárok:
60-tól 5
50-59 4
35-49 3
20-34 2
0-19 1
Ebben a dokumentumban megtalálhattok mindent, amit a geometriai transzformációk - egybevágósági transzformációk - Ismétlés rész feldolgozásához tudnotok kell.